Global mapping of kinematics and dynamics of tidal currents with surface drifters by Shane Elipot, Edward Zaron, Jonathan M. Lilly, and Rick Lumpkin.

Global mapping of kinematics and dynamics of tidal currents with surface drifters by Shane Elipot, Edward Zaron, Jonathan M. Lilly, and Rick Lumpkin.

Anyway, the slogan for this decade is “The Science We Need For the Ocean We Want”. I don’t think this rolls easily on the tongue, but I think it means that it will be up to us to decide what we want to do as scientists to fulfill the Ocean Decade Challenges (perhaps). As the decade is an international activity, it is not a funding program but rather a framework to work together to create new ideas and solutions. One of the ways this will be achieved is by the Decade endorsing specific Decade Actions for which there is a call, closing on 15 January 2021.
This decade has been in preparation since 2017 thanks to the work of The Intergovernmental Oceanographic Commission (IOC) of UNESCO, the United Nations Educational, Scientific, and Cultural organization. IOC has produced an Implementation Plan for the Decade, now in its version 2.0 (took me a while to find the link). This plan lists 7 Outcomes (that’s the ocean we want), and as a physical oceanographer, I guess I am interested in Outcome #4 (A predicted ocean where society understands and can respond to changing ocean conditions) and Outcome #6 (An accessible ocean with open and equitable access to data, information and technology and innovation). But before we get to the outcomes of the Decade we will have to “fulfill” 10 Challenges, such as Challenge #5 which is to enhance understanding of the ocean-climate nexus and generate knowledge and solutions to [do a lot of stuff] , and Challenge #7 to Ensure a sustainable ocean observing system across all ocean basins that delivers accessible, timely, and actionable data and information to all users. Ambitious stuff. Then, there are also 3 Objectives, each of them with 5 to 7 Sub-Objectives and there I am starting to be a bit confused about the purpose of these … I am reading that they are to guide the development and delivery of Actions towards the fulfilment of the Decade Challenges …
If you are still reading this, and you are based in the USA, you should perhaps know that the National Academies of Sciences, Engineering, and Medicine (NASEM) will serve as the organizational center for coordination of scientific initiatives to inspire U.S. contributions to the Decade (note that the Academies are private, nonprofit organizations, so not governmental and thus non partisan). Notably, NASEM has established a US National Committee to convene activities related to the Decade. As such, the US Committee has issued a call for submission of “Ocean-Shots”. As a non-native English speaker working in the US, I really had no idea what that referred to. Then I heard it is related to the concept of Moonshot, which according to urbandictionary.com is awesome, fantastic, almost impossible to achieve, the best, the reason for success, reaching the highest point, right on target … Note that I am not quite sure how this Ocean-Shot application or concept will fit into the call for Decade actions and the Decade endorsement.
In any case, with the support of Rick Lumpkin from NOAA/AOML, Luca Centurioni from Scripps Institution of Oceanography, and Josh Willis from NASA/JPL, I have submitted an Ocean-Shot application to NASEM about the idea/concept of implementing a new global ocean observing system for mean sea level, based on my latest paper published in AGU GRL [1] and featured in AGU’s EOS as a Research Spotlight. This is kind of a crazy idea, and realizing this idea will require national and international collaborations … and help. So I thought it would be a good idea to put it out there in the open, for the sake of #openscience, and I hope to gather ideas, suggestions, and criticisms. Let me know what you think by email selipot@miami.edu, twitter, or use Disqus below to post your comments.

1. Abstract (describe hypothesis, scientific and/or technological objectives, 200 words limit)
We propose to establish a new ocean observing system for monitoring global and regional mean sea level changes. This system will consist of a global array of thousands of water following drifting buoys tracked by a global navigation satellite system—such as the Global Positioning System (GPS)—which will continuously provide the geographical positions and the height of the sea surface along the buoys’ trajectories. The sea level height data collected in this way, averaged over regional basins and the global ocean, will provide daily measures of regional and global mean levels. An essential climate variable, mean sea level is an intrinsic measure of climate change, integrating the thermal expansion of the ocean’s waters and additions to the ocean’s mass from melting terrestrial ice. The realization of this new system requires that standardized vertical position measurements with controlled accuracy be acquired and regularly transmitted from relatively small and expendable drifting buoys, which constitutes a technological challenge, yet one with a clear path for being met. The development and implementation of this ocean shot concept will ultimately provide an independent, resilient, sustainable, and economical observational system to quantify natural and anthropogenic sea level changes, augmenting the existing satellites and tide gauge observing systems.
2. Relevant Ocean Decade Challenge(s):
This ocean shot concept is related to Challenge 5 since it contributes to the understanding of climate dynamics by measuring mean sea level; to Challenge 6 since it provides a near-real time monitoring of regional and global mean sea level; to Challenge 7 since it consists of a global ocean observing system delivering free and immediately accessible data to all potential users; and to Challenge 8 since it delivers its data in near-real time to reveal a dynamic monitoring of regional and global mean sea level.
3. Vision and potential transformative impact (200 word limit):
Currently, global mean and regional sea level changes are monitored by two observational systems: coastal and island tidal gauges and satellite radar altimeters. Tidal gauge records have high temporal resolution, but their representativeness of the global mean sea level is biased toward the coasts and the Northern Hemisphere. In contrast, the altimeter reference record is almost global but can only provide a near-synoptic view about every 10 days and spatial resolution of hundreds of kilometers. The envisaged observing system will be high frequency, such as daily, and it will be global by notably including the highest latitudes such as in the Arctic ocean. The new system will be independent of the other systems, but also resilient and scalable, fit-for-purpose and economical, rapidly deployable and adaptable to new technologies and scientific objectives related to understanding and adapting to the threat of the sea level rise and climate change. Importantly, the new system will introduce an important redundancy that would preserve the continuity of the record in case of failure of key satellite missions.
4. Realizable, with connections to existing U.S. scientific infrastructure, technology development, and public-private partnerships (150 word limit):*
A global network of drifting buoys already exists in the form of the Global Drifter Program (GDP), the principal component of the international Data Buoy Cooperation Panel. The GDP is sustained by US federal agencies, with engagements from other countries. The proposed observing system could be quickly deployed by enhancing the positioning technology of GDP drifters, adding to its scientific value and expanding its existing objectives by adding the capability to measure mean sea level. The GDP buoys already use GPS technology to measure surface currents together with sea surface temperature, atmospheric pressure and, and for some, salinity, providing an oceanographic context to new sea level measurements. Importantly, the GDP readily provides the framework for technological development by Scripps Institution of Oceanography and other commercial companies already building drifters, and the logistical infrastructure for deployment and data processing by the Atlantic Oceanographic and Meteorological Laboratory.
5. Scientific/technological sectors engaged outside of traditional ocean sciences (100 word limit):
A recent study (Elipot, 2020, doi:10.1029/2020GL091078), demonstrate that, with the current characteristics of the existing GDP array of 1250 drifters, global mean sea level decadal linear trend estimates with an uncertainty less than the recommended 0.3 mm per year could be achieved with daily random error of 1.6 m or less in the vertical direction for each individual drifter daily estimate. With a pilot project currently underway, this technological challenge will be overcome by combining research and development in global navigation satellite system science, signal processing, and geodesy.
6. Opportunities for international participation and collaboration (100 word limit):
The accuracy of measuring global mean sea level change from an array of drifting buoys improves not only with the individual vertical accuracy of a drifter height measurement, but also with the number of active drifters (Elipot, 2020). Just like the current GDP relies on international collaborations for buoy deployments in the world’s ocean, the proposed array will also need international participation for its implementation and funding. As such, the ultimate scale of the proposed observing system constitutes a clear example of the application of slogan “the science we need for the ocean we want”.
7. Builds global capacity and encourages the development of the next generation of ocean scientists (100 word limit):
Globally distributed deployments of buoys by international partners, and the associated stream of oceanographic data, provide opportunities for personal, institutional, and community engagements. As an example, sea level and other data from a single buoy could relatively easily be apprehended by a single investigator or student. Such individual engagement could ignite further investigations which would include a large number of drifters requiring wider coordination and expertise through a multi-people project, building into the global capacity of the proposed system.
References
]]>So, I have decided to write a little note to demonstrate why variance-preserving spectra should not be used to make conclusive statements about periodicity in a time series, and to suggest alternative methods. I have recently become a research assistant professor, and thus I am trying to get a bit more in the teaching side of things (I do not teach at my institution which is what the research epithet means). So here you go, I writing this blog post to give some pointers. Let me know if I am doing it all wrong at selipot@rsmas.miami.edu or please comment below.
One definition of the frequency spectrum \(S(f)\) (there are several) is that it is the Fourier transform of the autocovariance function \(R(\tau)\), or in other words, that the spectrum and the autocovariance function are Fourier transform pairs:
\[S(f) \equiv \int_{-\infty}^{+\infty} e^{-i 2 \pi f \tau} R(\tau) d\tau , \quad\quad R (\tau) = \int_{-\infty}^\infty e^{i 2 \pi f \tau} S(f) \, df .\]This is called the Wiener–Khintchine theorem (the spelling of Khintchine varies). When the expression above is evaluated at zero lag \((\tau=0)\), one obtains that the variance of your time series, \(\sigma^2\), is the integral of the frequency spectrum:
\[\sigma^2 \equiv R (0) = \int_{-\infty}^{+\infty} S(f) \, df .\]This is why I personally think estimating a spectrum is the most useful: it shows the frequency decomposition of the variance of your time series. It allows you to state something about where the energy of your signal resides. If you are new to spectral analysis you could start with my lecture on time series analysis or the entire course on the subject by my colleague oceanographer Jonathan Lilly. At the bottom of this post you will find also some good book references including the excellent Percival and Walden (1993) Spectral Analysis for Physical Applications.
Now to the topic of this post: another typical use of spectral (or harmonic) analysis in physical oceanography is to look for quasi-periodic signals in a time series, such as a seasonal or an annual cycle. People are looking for “peaks”, which amounts to looking for patterns in a time series. This seems to be a very human trait because in oceanography exactly periodic signals are actually rare, and purely monochromatic signals (one frequency) even more so. As a side note, a typically erroneous interpretation of a spectrum I often hear is about a semi-annual peak (6-month period). Typically the reason for such a peak is not that there is a physical process at that specific frequency, but more likely that it is a harmonic of the annual, and lower, frequency. In other words you have a periodic signal with a 1-year period but it is not a pure sinusoid, and more than one frequency is needed to describe the periodic process (That’s the principle of Fourier series decomposition).
Here I want to show a synthetic example of a time series that is not unlike many published oceanographic time series, and show how a variance-preserving spectral plot of this time series can lead to misidentifying peaks. Below is shown a randomly generated real-valued time series with \(1000\) points. I generated and scaled this time series so that its variance is \(0.01\) and thus its standard deviation is \(0.1\):
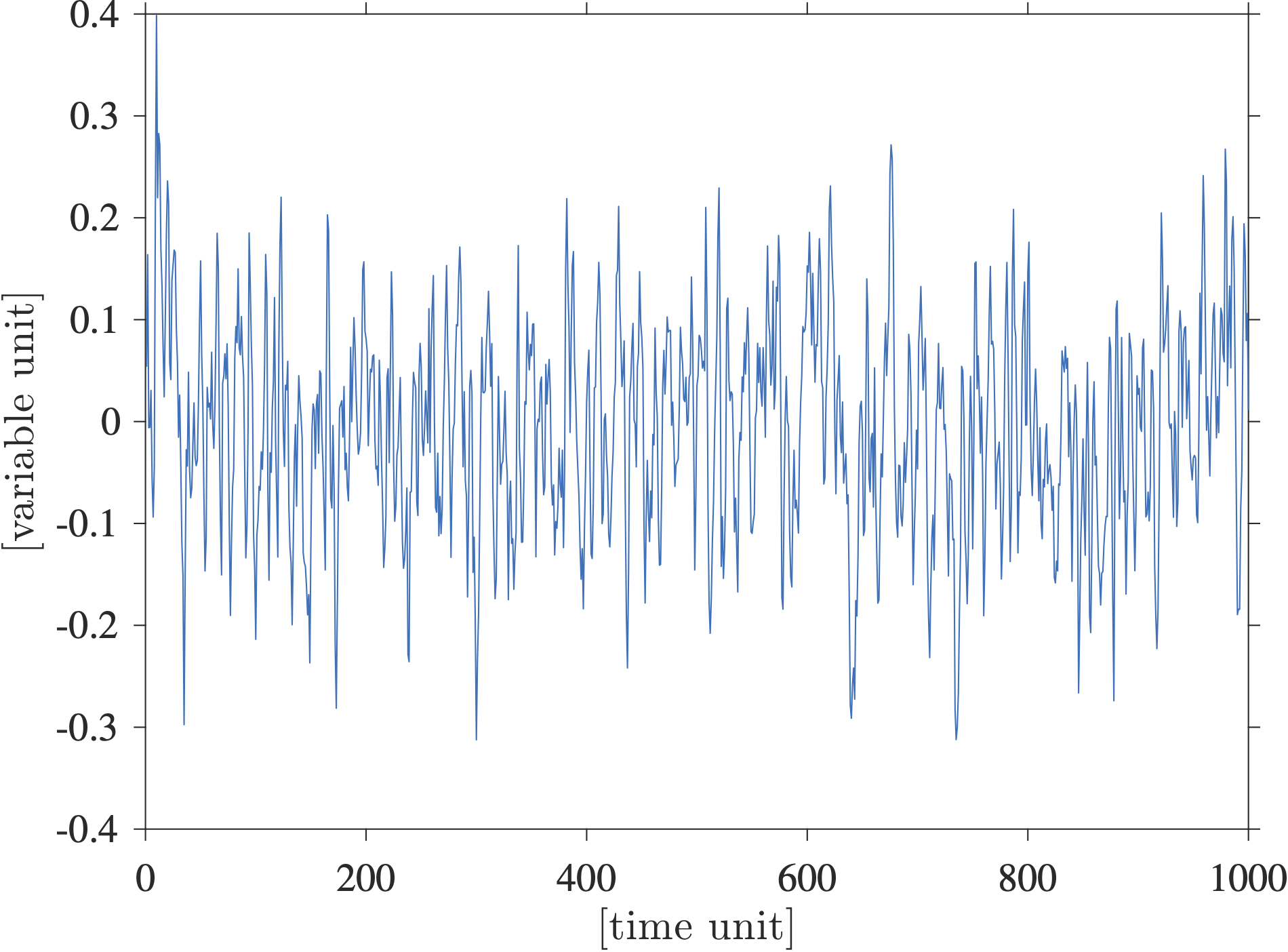
This time series is actually one realization of a Matérn process with a spectrum given by
\[S(f) = C \frac{A^2}{[(2\pi f)^2+\lambda^2]^\alpha}\]where \(C\) is just a normalizing constant. To generate this time series I used a freely accessible Matlab toolbox called jLab written by Jonathan Lilly. I like this model because it fits nicely a lot of oceanographic time series I have looked at, including Lagrangian time series and time series of oceanic transports. In fact, I have used that model to conduct some testing on the statistics of transport time series of the AMOC in my Elipot et al. 2017 paper. The point of using this model is that there is absolutely no periodicity in this signal; it has a continuous spectrum with no peak. What does a peak in a spectrum mean anyway? I think it should mean that the spectral power at a single frequency is much greater than neighboring frequencies, or that it is much more than what you would expect under the hypothesis that your observed process (i.e. time series) is representative of some noise-like process, white or colored. There is nothing wrong with a noise-like process by the way, on the contrary it tells you a lot about your observations.
Now, how does a spectral estimate of this time series look like? The next figure shows a multitaper spectral estimate which is really one of the best methods around to estimate a spectrum in a non parametric way (i.e. not knowing its shape, see my lecture as an example on how to implement it practically). The estimate is shown in blue, the non-symmetric 95% confidence intervals are shown in lighter blue, and the theoretical spectrum is shown in red.
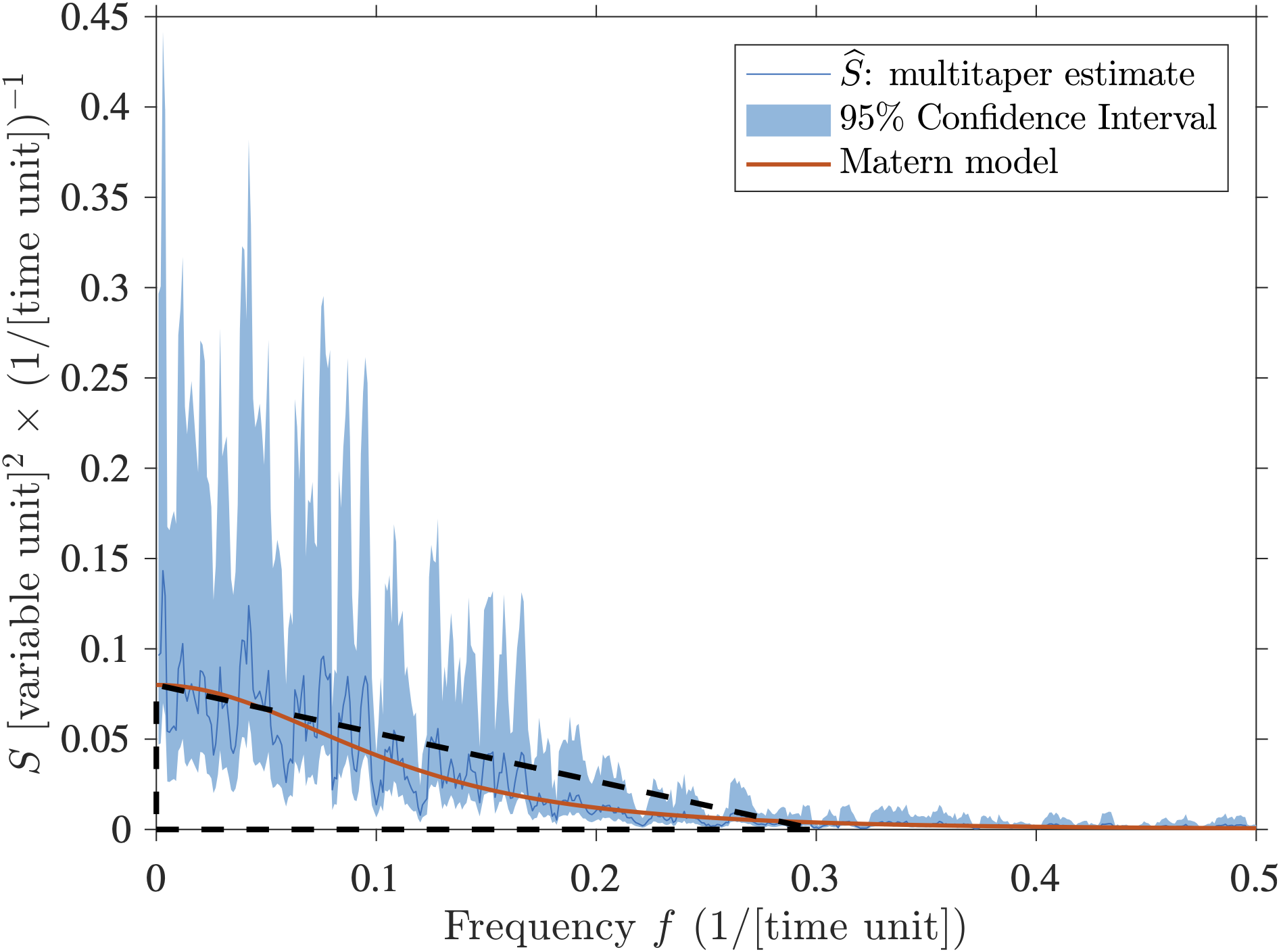
You may say that the estimate in blue is very different from the true spectrum in red. That is however the nature of spectral estimation using finite time series. There is no added noise in the time series, only the process described by the theoretical spectrum. From discrete and limited data, the true spectrum is not accessible, it can only be estimated, sometimes poorly. By the way, with this plot, if you have scaled your spectrum properly, you can probably estimate the variance of the signal since it is the area under the curve according to the Wiener–Khintchine theorem given above (Here I would eyeball that the area under the spectral estimate is about the area of the drawn triangle so approximately \(\frac{1}{2} \times (0.08 \times 0.3) \approx 0.01\) which is the variance I specified above).
Now, because the variance of a typical time series in oceanography spans a very wide range of magnitude over a wide range of temporal scales, it is typical to plot a spectrum on a so-called log-log plot, that is with the two axes shown on a logarithm base 10 scale:

I am sure this type of spectrum looks very familiar to many: a plateau towards the zero frequency, a shoulder break at mid-frequencies, and a power-law behavior at higher frequencies that manifests itself as a linear slope in this log-log representation. One issue with such log-log plot is that it really emphasizes the lowest frequencies which are nothing special compared to all the other ones in a statistical sense. However, we care about the lowest frequencies because we are often interested in long time-scale processes. We typically received funding to collect an oceanographic time series for as long as we could and really would like to know about the period as long at the length of our experiment (hence I suggest the use of the multitaper that can achieve that, and not the Welch’s method or any method that chop your time series in segments). Cool, now, see any peaks? Maybe, but really, there are none by construction.
So now, let’s consider a variance-preserving spectrum instead (sometimes also called an area-preserving plot). Such plot has nothing to do with the estimation of the spectrum itself, it’s just a different kind of plot. A google search leads to a note written by my PhD advisor (who knows a lot about statistics) about what that beast is. I think it is also described in Emery and Thompson, as well as in Carl Wunsch’s primer on time series analysis. Now, using the fact that \(d(\ln(f)) = df/f\), one can rewrite
\[\sigma^2 = \int^{+\infty}_{-\infty} S(f) df = \int^{+\infty}_{-\infty} S(f)\, f d(\ln(f))\]Here, \(\ln\) is the natural logarithm (logarithm base \(e\)) not the common logarithm (base 10). The idea behind this transformation is that when one plots \(S(f) \times f\) on the “y axis” versus \(\ln(f)\) on the “x axis”, the area under the curve between two frequencies is proportional to the variance in the range of frequencies defined by these two frequencies. It compensates for the “squeezing” of the high frequencies and the “stretching” of the low frequencies in the previous plot above. So now a variance-preserving version of the previous plots is:
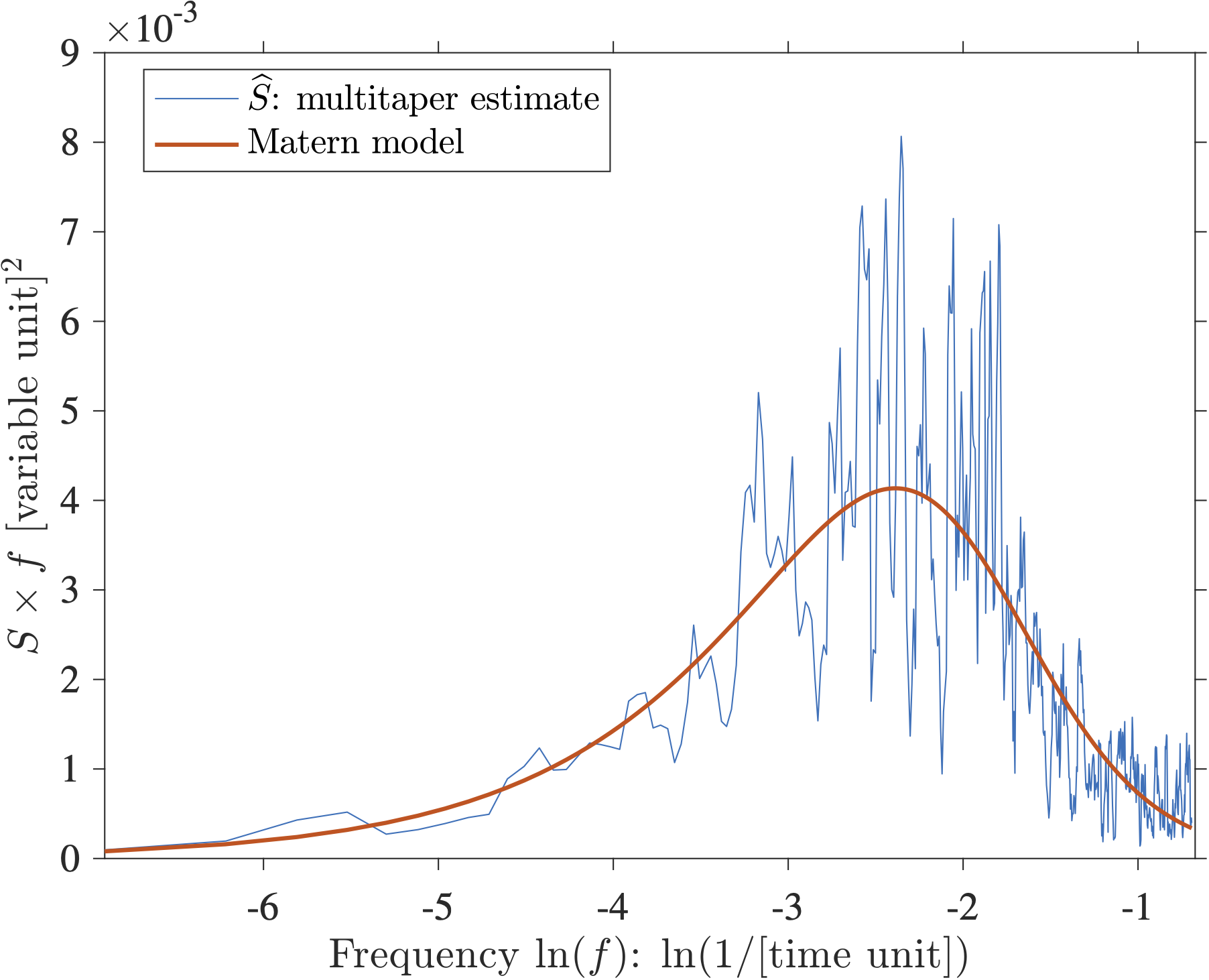
In this plot the y-axis is in units of variance of your variable, and the x-axis is this weird logarithm unit. So now, see any peaks? Well, maybe there are peaks between \(-2\) and \(-3\)? Even the theoretical spectrum would suggest that there is a “hill” near that range of frequencies … wouldn’t that be a peak? Nope. Nevertheless, the frequencies near that hill are the frequencies for which the Matérn process transitions from a “white” (flat) type of spectrum to a power-law (self-similar) type of spectrum. This range of “transition” frequencies is actually controlled by the damping parameter \(\lambda\) of the theoretical spectrum (see equation above). If you’d like to know more, you could read Lilly et al. 2017.
But in the end, there are no peaks. Unfortunately, I have seen many papers claiming that peaks existed solely on the basis of a plot just like the one above. I think a variance-preserving spectrum is actually very misleading when investigating periodicities. I don’t recall reading any papers that use this representation for the purpose of using the area under the spectral curve to relatively quantify the distribution of variance.
So, in the end, how does one look for peaks? I don’t think I have ever published a paper without a spectral estimate in it and I am still approaching this question with apprehension. I still think that it is not simple and this should be the subject of another post (hopefully the next one). One could start however by using the confidence intervals as there are established formulas to calculate those! Given the confidence intervals displayed in the linear or logarithmic plots shown above, one could qualitatively say that there are no outstanding peaks in this example. Otherwise, I personally use a statistical test for periodicity in colored noise given by Thomson (1982) and described nicely in Percival and Walden, (1993). Peaks in colored noise is the most common situation I have encountered in physical oceanography. I have coded it in Matlab, send me an email and I’d be happy to share.
The Matlab script to generate the figures above is available at a GitHub repository. My apologies for still using a proprietary computation software. I think that script should also work in the free Matlab-look-alike Octave software but I have not tested it.
References
[3] Jenkins, G.M. and Watts, D. G. (1968), Spectral Analysis and its Applications, Holden-Days.
]]>My audience was broad and diverse (more than 30 students!), from Masters level to postdoctoral researchers. I am pleased to make now available openly on my website the slides of these five lectures, as well as the Matlab scripts that the students worked with during afternoon practical sessions. I was ambivalent about making the students use a commercial software, as opposed to an open source software like Python. However, In the interest of time and exactness, I had to stick to what I knew. In addition, most of these Matlab scripts are compatible with the Matlab-like free software Octave.
By the way, I am always grateful to Jonathan Lilly who made me embark on this journey of lecturing on stats! And please check out the latest version of his course on time series analysis here.
Please feel free to email me with comments or questions about this material!
]]>This 1.01 update adds newer data to the previous version, one year of quality-controlled data up to 30 June 2016 for Argos-tracked drifters, and more than one year of GPS-tracked data, up to 1 October 2016. In addition, we have added data before 1 September 2005 (the start date of version 1.00) by considering all GPS-tracked drifters since the beginning of the GDP, and all Argos-tracked drifter data since the beginning of the GDP, when the average of the uneven sampling intervals per trajectory is less than or equal to 3 hours.
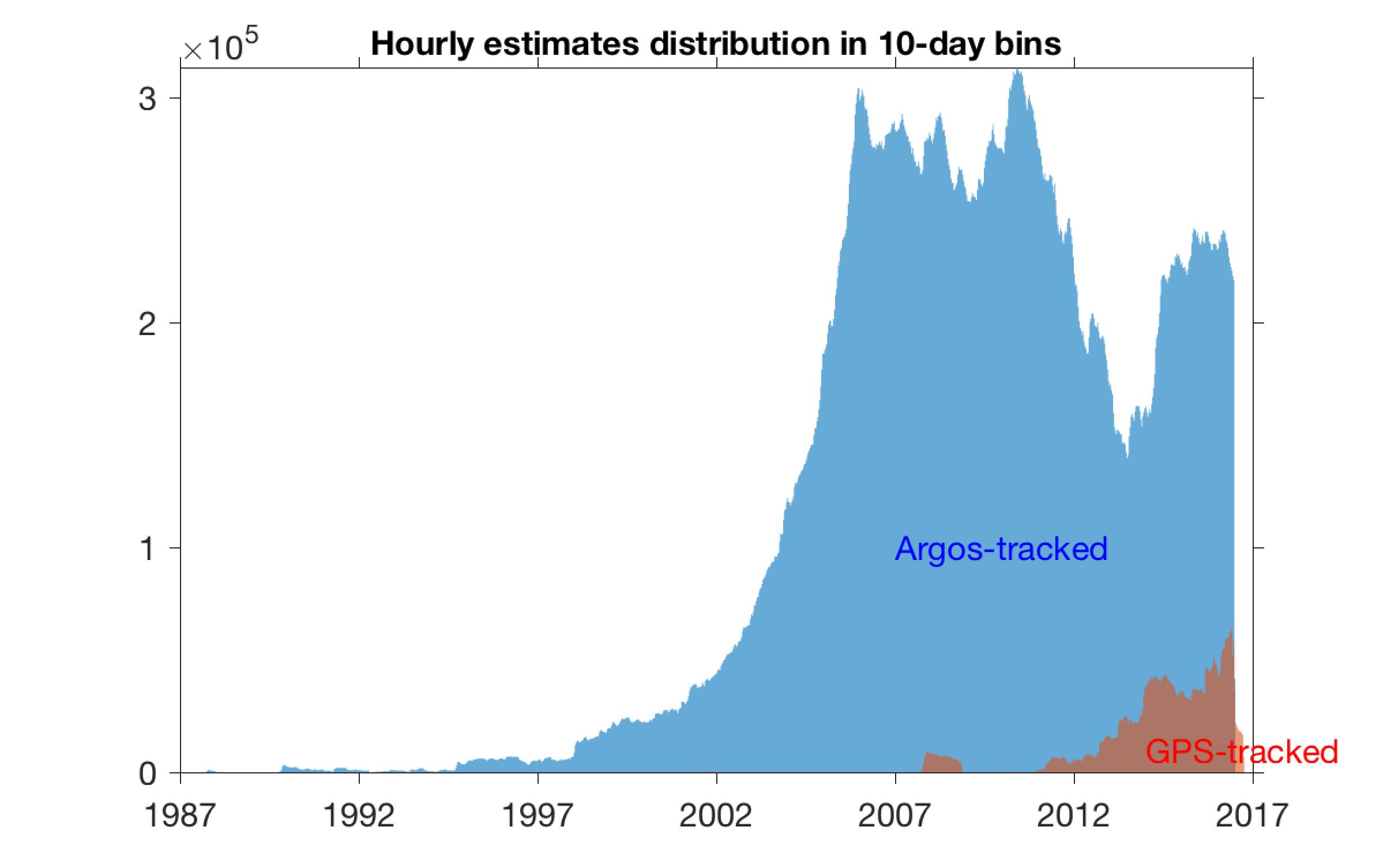
The 1.01 dataset now totals over 117.4 million estimates of position and velocity with confidence intervals from 12,287 Argos-tracked drifter trajectories, and over 5.6 million estimates of position and velocity with confidence intervals from 985 GPS-tracked drifter trajectories.
Simplified versions of the Matlab codes used to generate this dataset are available through a GitHub repository.
]]>All you’ll own is earth until
You can paint with all the Colors of the Wind
Ocean
Thank you to Kim Martini for pointing out on twitter a new article published in Oceanography magazine! In that article, Thyng et al. present a set of freely available colormaps called cmocean to be used for oceanographic applications. This newish set strives to provide a selection of color palettes chosen to accurately serve the representation of data, with color hues we oceanographers traditionally associate with oceanic variables (such as deep blue to white for sea ice). The set is built in order for our eyes to not misinterpret the data being presented (the analog filter of our eyes perceive colors and color gradients unevenly). In particular, the method used by Thyng et al. consists in making sure the perceptual (visual) changes in a given colormap match the changes in the underlying data, using a property of color called “lightness”, and relies mostly on the viscm tool. Appropriately, The authors point out the pitfalls of the jet colormap (which I have always personally found evil), and I think they are right on point when assigning the apparent popularity of that colormap to having been the default MATLAB colormap for many years (but recently switched to the demure parula colormap by the way).
The business of colors can be incredibly complicated, but also very useful. I am very keen on using the phase information of data, which is a challenging thing to represent when an associated magnitude is also present. In several of my papers I have relied on the Hue-Saturation-Value (HSV) properties of colors rather than the more traditional Red-Green-Blue (RGB) representation (see as an example my 2016 paper Characteristics, Energetics, and Origins of Agulhas Current Meanders and their Limited Influence on Ring Shedding). Another example on the use of colors in oceanography is the paper by Hughes and Williams in 2010 called The color of sea level who smartly used colors to represent 3D information of sea level spectra on the globe.
So, check out this new paper and the refrences therein if you are interested in colors!: True Colors of Oceanography Guidelines for Effective and Accurate Colormap Selection (2016) By Kristen M. Thyng, Chad A. Greene, Robert D. Hetland, Heather M. Zimmerle, and Steven F. DiMarco, doi:10.5670/oceanog.2016.66
(Pocahontas is my second favorite Disney movie, yes, after The Little Mermaid) …
]]>What I found funny is that following this rejection one of his students introduced him to “Shit my reviewers say”, the excellent tumblr account which is also on twitter as @YourPaperSucks and has been a favorite of mine for some time. If you did not know this wonderful resource of procrastination, happy reading!
]]>Something new is happening though. Recently, as part of the last checks before one of our newest manuscript got accepted, we were asked by the journal editor to disclose the “availability of our code”. Obviously, stating that our messy, uncommented, code written for the commercial software MATLAB was not available, was not acceptable. I was first annoyed at the daunting task of putting together a sharable code but mostly I was surprised. I was surprised because our methods involved relatively standard statistical techniques and tools, and a few relatively unusual ones that were otherwise clearly referenced in our “methods” section. What I mean is that the references given in our article clearly spelled out the formulae used. As an example, I have become really fond of kernel estimators and the Nadaraya-Watson estimator with a Gaussian or an Epachnikov kernel has become my go-to for non-parametric curve estimation. The book Local Polynomial Modelling and Its Applications by Fan and Gijbels is a very nice introduction to these methods. So, in the end, not only do we have to say with words, or equations, what we did, but we also have to type it up for others. Isn’t that too much?
I am being sarcastic and it looks like this is the way forward anyway, so the old guard better adapt, and students better get acquainted right away with these methods. The goal is to improve reproducibility of results (especially in wet labs), and as such some journals have started to hire editors for that purpose. Thank you to my colleague Ryan Abernathey for tweeting this article. In addition, it apperas that one of the points of this movement is to improve the quality of scientific code. That means clear structure, organization, testing, comments, and documentation. Scripps graduate student Cesar rocha’s recent project is apparently a very good example. Another example is veteran oceanographer Jody Klymak is making available a lot of his analysis code through his GitHub page. Finally, my collaborator Jonathan Lilly at NorthWest Research Associates has been working very hard for many years to put together his superb Matlab Toolbox called Jlab. It is distributed through Matworks File Exchange but it is also on GitHub for suggesting edits and modifications. GitHub watch out, here I come. (This site is hosted by GitHub Pages).
]]>